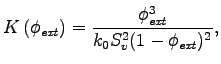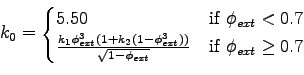Davies-Ingmanson

Constitutive Equations » Permeability » Davies-Ingmanson

Description

The relationship used by Ingmanson et al. (1959) is a further development to the widely-used Robertson-Mason relationship (Robertson and Mason, 1949). It enlarges Robertson-Mason relationship applicability region by taking into account the effect of the increasing Kozeny constant, $ k_0$ , for high values of porosity. An equation suggested by Davies (1952) is used to describe $ k_0$ dependence on porosity at high porosities.

Application

The applicability region of the Davies-Ingmanson relationship is limited at high concentrations by the same assumptions made by Robertson-Mason relationship regarding the effective volume being constant. The relationship is, therefore, not valid at fibre concentrations higher than 250 kgm (Wang et al., 2002). There is no limit at low concentrations according to the literature.

The relationship is recommended for forming and vacuum sections where fibre concentrations are below 250 kgm.

Background

Ingmanson et al. use the same equation as Robertson-Mason:

$\displaystyle K \left(\phi_\mathit{ext}\right) = \frac{\phi_\mathit{ext}^3}{k_0 S_v^2(1-\phi_\mathit{ext})^2},$    

where $ k_0$ is the Kozeny constant, $ S_v$ is the specific surface area and $ \phi_\mathit{ext}$ is the external porosity. However, Ingmanson et al. show with experiments that Kozeny constant, $ k_0$ , increases fast for increasing values of porosity. An equation first suggested by Davies is used to describe $ k_0$ dependence on porosity at high porosities:

$\displaystyle k_0 = \begin{cases}5.50 & \text{if $\phi_{ext} < 0.7$} \\ \frac{k... ...hi_{ext}^3))}{\sqrt{1-\phi_{ext}}} & \text{if $\phi_{ext} \ge 0.7$} \end{cases}$    

where $ k_1$ and $ k_2$ are parameters, which Ingmanson et al. estimated to be 3.5 and 57 respectively.

Bibliography

Davies, C. N., 1952, Proc. Inst. Mech. Engrs. .

Ingmanson, W. L., B. D. Andrews, and R. C. Johnson, 1959, Tappi Journal 42(10), 840.

Robertson, A. A., and S. G. Mason, 1949, Pulp Paper Magazine of Canada 50(13), 103.

Wang, J., A. N. Hrymak, and R. H. Pelton, 2002, Journal of Pulp and Paper Science 28(1), 13.

Back to Permeability