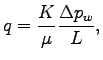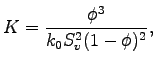Permeability

Constitutive Equations » Permeability

One of the most used constitutive equation in papermaking is the permeability, which is widely used to describe fluid flow through a porous medium, viz. the fibre network, which later at the end of the paper machine becomes the final product, the paper.

Permeability, $ K$ , connects the fluid flux, $ q$ , alternatively, the fluid velocity, to the hydraulic pressure difference, $ \Delta p_w$, according to Darcy's equation:

$\displaystyle q = \frac{K}{\mu}\frac{\Delta p_w}{L},$    

where $ L$ is the medium length and $ \mu$ is the fluid viscosity. Permeability depends on the internal structure of the medium, therefore it is often expressed as a function of the porosity. For compressible medium it is often important to express permeability as a function of the local porosity. This effect is often taken into account in papermaking modelling.

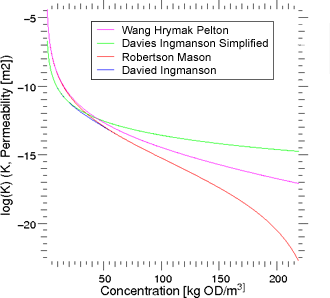
A large portion of the relationships used in papermaking to describe the dependence of permeability with porosity can be divided in two main groups, viz. relationships based on the hydraulic radius and power law relationships.

Hydraulic-Radius Based Relationships

The relationships from this group are mostly used in the initial parts of the paper machine at relatively high porosities. All the available relationships in PaperSim within this group are derived from Kozeny-Carman equation:

$\displaystyle K = \frac{\phi^3}{k_0 S_v^2(1-\phi)^2},$    

where $ k_0$ is the Kozeny constant, $ S_v$ is the specific surface area in contact with the fluid and $ \phi$ is the porosity. The following relationships are available in PaperSim:

Power-Law Relationships

The relationships from this group were obtained empirically, and are usually of the form

$\displaystyle K = a\phi^b,$    

where $ a$ and $ b$ are empirical constants. The different equations appear through the replacement of the porosity for another measure of state of the internal structure of the medium. The relationships from this group are mostly used in later parts of the paper machine at relatively low porosities. Among them, the following are available in PaperSim:

  • Power-law
  • Nilsson-Larsson

Permeability

permeability

Comparison between four different constitutive equations for permeability as a function of concentration. In all cases it was assumed the specific external surface area, Sw = 910 kg/m3 and the specific swollen volume, α = 4.20×10-3 m3/kg