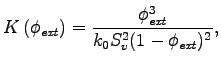Wang-Hrymak-Pelton

Constitutive Equations » Permeability » Wang-Hrymak-Pelton

Description

The Robertson-Mason relationship and several of the derivative relationships based on it assume constant effective volume. Therefore, they have the drawback of underestimating permeability at low porosity. This is due the fact that they assume the volume occupied by the swollen fibres to decrease with compression. In fact, all these relationships predict negative permeability for high enough concentrations. In order to cope with this problem, (Wang et al., 2002) proposed an expression for the dependence of the external porosity on concentration that does not allow it to reach zero irrespective of the concentration.

Application

The applicability region of the Wang-Hrymak-Pelton relationship extends the Robertson-Mason relationship at high concentrations. The Wang-Hrymak-Pelton relationship is, therefore, only limited at low concentrations as $ k_0$ was assumed to be constant. According to Ingmanson et al. (1959), $ k_0$ raises fast at external (available for flow) porosity higher than 0.7. There is, however, no impediment that the equation proposed by Davies (1952) to be used with the Wang-Hrymak-Pelton relationship in order to cover the full range of concentration (see the Davies-Ingmanson relationship).

There is no theoretical restriction with respect to the operation region where the Wang-Hrymak-Pelton relationship can be deployed.

Background

Robertson and Mason (1949) were first to introduce swollen fibre properties to Kozeny-Carman equation. They derived the equation:

$\displaystyle K \left(\phi_\mathit{ext}\right) = \frac{\phi_\mathit{ext}^3}{k_0 S_v^2(1-\phi_\mathit{ext})^2},$ (1)

where $ k_0$ is the Kozeny constant, and estimated to 5.55. $ S_v$ is the specific surface area - i.e. the external area per unit volume - in contact with the fluid and $ \phi_\mathit{ext}$is the external porosity, i.e. the ratio between the volume available for flow and the total volume.

Robertson-Mason relationship has the drawback of underestimating permeability at low porosity as the volume occupied by the swollen fibres does decrease with compression. Eventually $ \phi_\mathit{ext}$reaches zero and negative values for high enough concentrations. Therefore, Wang et al. proposed the following equation instead:

$\displaystyle \phi_\mathit{ext} = \left(1 -\theta\right)^{\gamma c},$ (2)

where $ \theta$ is the volume fraction of swollen fibre at concentration of 1.0 kg. $ \gamma$ is a parameter introduced just to make the exponent dimensionless. The limitations from Robertson-Mason relationship at high concentrations are removed, as $ \phi_\mathit{ext}$never reaches zero according to Equation (2).

Bibliography

Davies, C. N., 1952, Proc. Inst. Mech. Engrs. .

Ingmanson, W. L., B. D. Andrews, and R. C. Johnson, 1959, Tappi Journal 42(10), 840.

Robertson, A. A., and S. G. Mason, 1949, Pulp Paper Magazine of Canada 50(13), 103.

Wang, J., A. N. Hrymak, and R. H. Pelton, 2002, Journal of Pulp and Paper Science 28(1), 13.

Back to Permeability