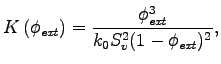Robertson-Mason

Constitutive Equations » Permeability » Robertson-Mason

Description

The Robertson-Mason relationship was the first to introduce swollen fibre properties to the Kozeny-Carman equation (Robertson and Mason, 1949). It assumes the specific surface, $ S_v$ , the effective volume, $ \alpha$ of the water swollen fibres and the Kozeny constant, $ k_0$ , to be constant.

Application

The applicability region of the Robertson-Mason relationship is limited at high and low concentrations by the assumptions mentioned above. At high concentration it is limited by considering effective volume to be constant. The relationship is, therefore, not valid at fibre concentrations higher than 250 kgm (Wang et al., 2002). At low concentrations it is limited by considering $ k_0$ to be constant. According to Ingmanson et al. (1959), $ k_0$ raises fast at external (available for flow) porosity higher than 0.7.

The relationship is recommended for forming and vacuum sections provided the concentrations involved are mostly within the range given above.

Background

Several relationships that have been proposed were based in the Kozeny-Carman equation (e.g. Bear, 1972). Robertson and Mason (1949) were first to introduce fibre properties to Kozeny-Carman equation. They derived the equation:

$\displaystyle K \left(\phi_\mathit{ext}\right) = \frac{\phi_\mathit{ext}^3}{k_0 S_v^2(1-\phi_\mathit{ext})^2},$    

where $ k_0$ is the Kozeny constant, and estimated to 5.55. $ S_v$ is the specific surface area - i.e. the external area per unit volume - in contact with the fluid and $ \phi_\mathit{ext}$is the external porosity, i.e. the ratio between the volume available for flow and the total volume. As a function of the concentration, $ c$, it is expressed as:

$\displaystyle \phi_\mathit{ext} = 1 -\alpha c,$    

where $ \alpha$ and $ S_v$ are a property of the fibre cake, and can be determined experimentally by different methods.

Bibliography

Bear, J., 1972, Dynamics of Fluids in Porous Media (Dover, New York).

Ingmanson, W. L., B. D. Andrews, and R. C. Johnson, 1959, Tappi Journal 42(10), 840.

Robertson, A. A., and S. G. Mason, 1949, Pulp Paper Magazine of Canada 50(13), 103.

Wang, J., A. N. Hrymark, and R. H. Pelton, 2002, Journal of Pulp and Paper Science 28(1), 13.

Back to Permeability