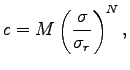Campbell

Constitutive Equations » Stress-Strain » Campbell

Description

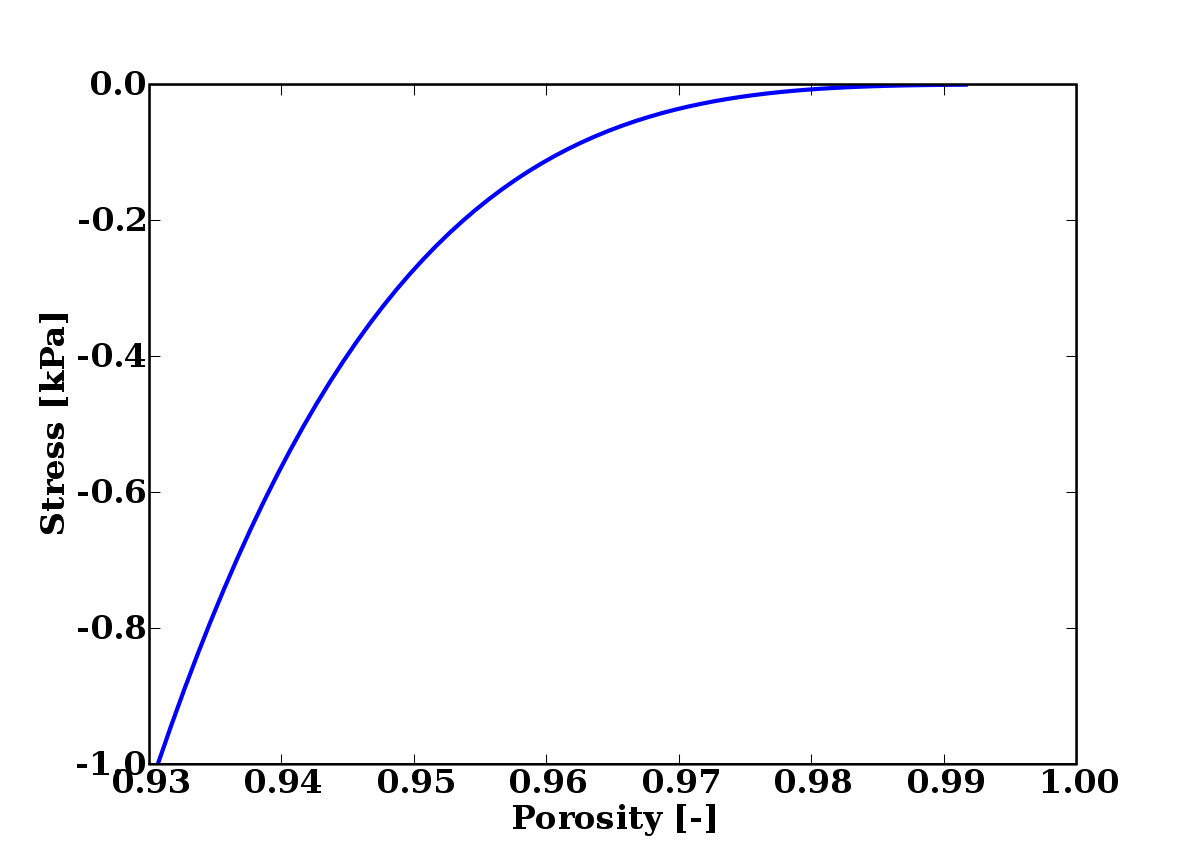
The simple power-law relationship first proposed by Campbell is the most widely used equation to describe the stress-strain in the fibre network.

Application

Campbell relationship describes well the stress-strain behaviour of fibre network for individual compression or relaxation, but not for cycles of compression and relaxation. Regarding concentration, Campbell relationship is applicable between the gel point and fibre concentrations at where water flows out of the fibre walls (i.e. at approximately 20 percent dryness).

It is therefore suitable in the forming and vacuum sections.

Background

The Campbell relationship was elaborated from empirical data (Campbell, 1947). It describes the concentration as a power function of the applied stress, $ \sigma$ :

$\displaystyle c=M \left(\frac{\sigma}{\sigma_r}\right)^N,$    

where $ c$ is the concentration, $ \sigma_r$ is a reference stress and $ M$ and $ N$ are fitting constants. $ \sigma_r$ is introduced just to avoid complex units in $ M$ . Gren and Ljungkvist (1983) show how the parameters $ M$ and $ N$ change with different pulp proprieties.

Bibliography

Campbell, W. B., 1947, Pulp and Paper Magazine of Canada 48(3), 103.

Gren, U., and K. Ljungkvist, 1983, Cellul. Chem. Technol. 17(Sep-Oct), 515.

Back to Stress-Strain

Campbell

Campbell

The Campbell constitutive equation for stress as a function of concentration (expressed here by the porosity). For the Campbell relationship the stress disappears only when there is no fibre left in the suspension.